ModernBERT's context-free embeddings
I've already written about a bit about visualizing BERT's context-free tokens. I recently had to do some work with the ModernBERT model, and thought that it might be fun to run the visualization scripts I had prepared for that model as well.1
For implementation details and such, you should read the BERT visualization, but in short the picture below has the ~50k input embedding vectors of the modernBERT model projected with three methods: PCA, t-SNE and UMAP. I've colored some tokens related to numbers.
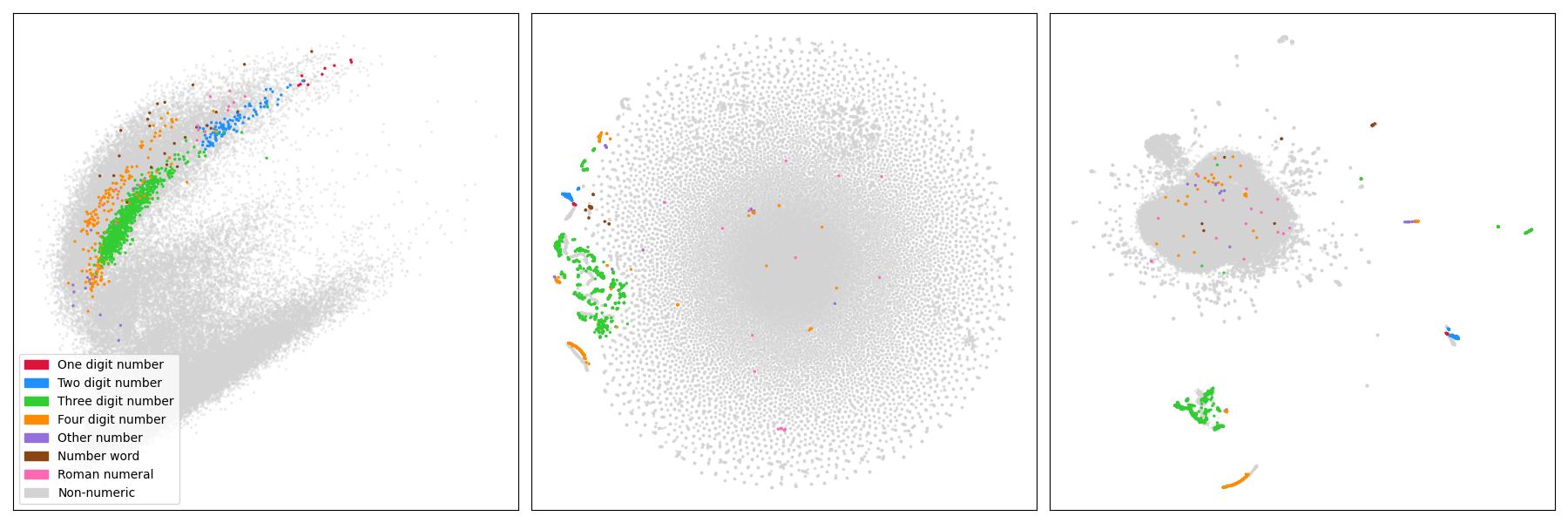
What I find striking is that despite the obvious differences to the vanilla BERT model, there are obvious similarities as well in the structure! Below we have the same image for the ~30k input embedding vectors of the BERT model.
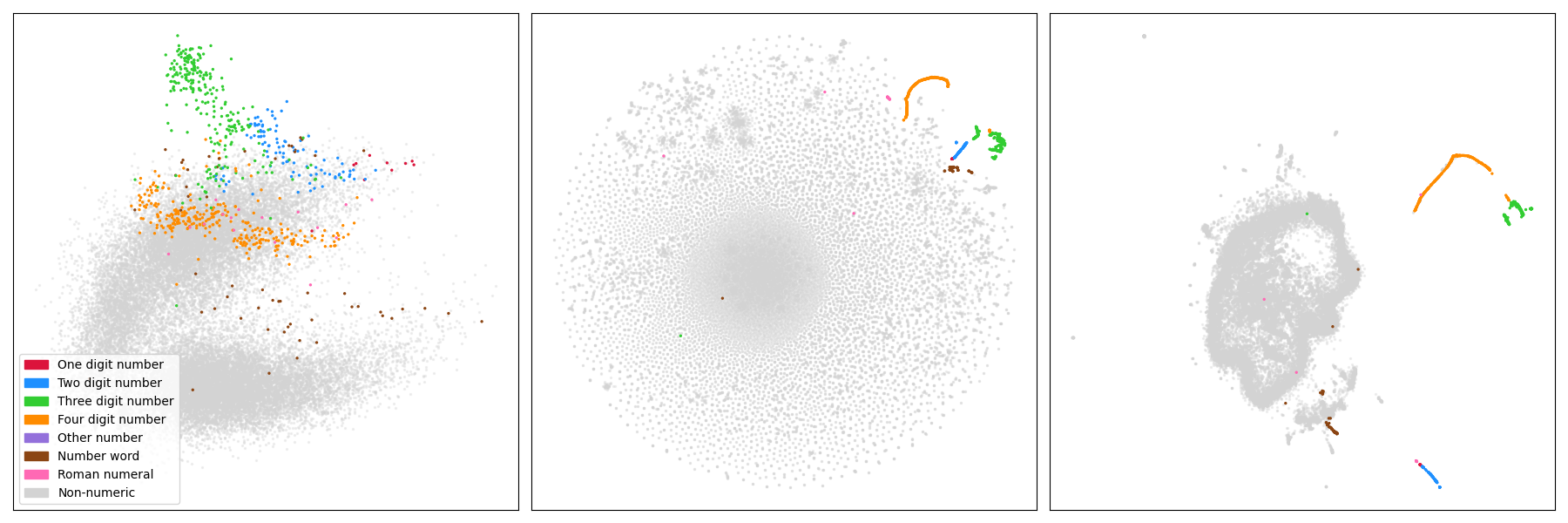
Indeed, both of the embedding collections have a vaguely Pacman-like shape w.r.t. the PCA projection, the t-SNE projects both of them to something that looks to me like a petri dish, and the UMAP (while more different than the others) has a larger component with separate smaller components, some of which seem to be the embeddings of numerical tokens in a somewhat one-dimensional geometrical structure.
This is surprising also due to the fact that the amount of tokens differ. Compared to the ~30k tokens of the original BERT system, the ModernBERT sports almost a double amount of tokens, around ~50k of them. In ModernBERT there are around a hundred (i.e. about 0.2%) which were quite long, over 32 characters, but they are just repeated symbols like - or *. Though quite many of them were repetitions of the Ġ symbol, i.e. the "don't prefix this token with a space" symbol, which I find odd.
Anyway, filtering out any token with length over 32, we get the following distributions of token lengths in the BERT and ModernBERT tokenizers.
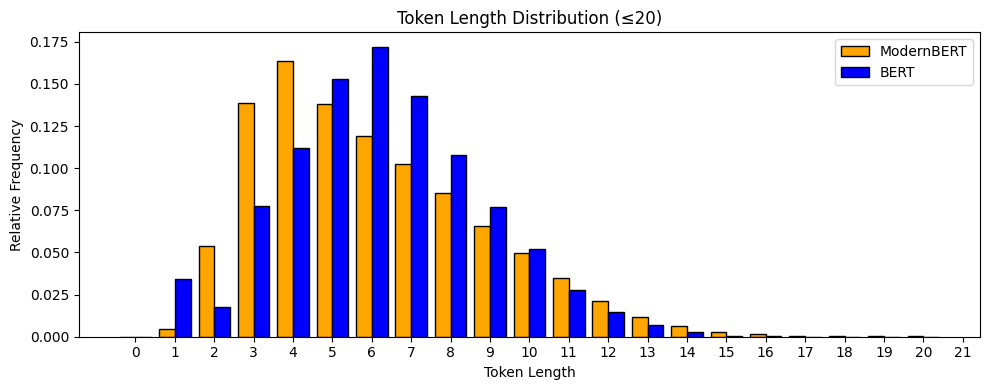
ModernBERT seems to have a slight preference for smaller tokens. I wonder if this is unexpected or not? It might be fun to plot how this kind of distribution evolves as you increase the vocabulary budget.
With this difference in token distributions we can also check which numbers have been priviledged enough to earn their own tokens:
Number of 1-digit numbers that are tokens: 10
Percentage of 1-digit numbers that are tokens: 100.00%
Number of 2-digit numbers that are tokens: 100
Percentage of 2-digit numbers that are tokens: 100.00%
Number of 3-digit numbers that are tokens: 877
Percentage of 3-digit numbers that are tokens: 87.70%
Number of 4-digit numbers that are tokens: 197
Percentage of 4-digit numbers that are tokens: 1.97%
Number of 5-digit numbers that are tokens: 6
Percentage of 5-digit numbers that are tokens: 0.01%
These tokens are:
00000, 10000, 14514, 00001, 12345, 80211
Number of 6-digit numbers that are tokens: 3
Percentage of 6-digit numbers that are tokens: 0.00%
These tokens are:
000000, 000001, 100000
Number of 7-digit numbers that are tokens: 1
Percentage of 7-digit numbers that are tokens: 0.00%
These tokens are:
0000000
Number of 8-digit numbers that are tokens: 5
Percentage of 8-digit numbers that are tokens: 0.00%
These tokens are:
00000000, 11111111, 14514500, 00000001, 99999999
The vanilla BERT model only extended token priviledges up to 4 digit numbers:
| Number Length | BERT tokens | modernBERT tokens |
|---|---|---|
| 1 digit | 10 | 10 |
| 2 digits | 100 | 100 |
| 3 digits | 258 | 877 |
| 4 digits | 304 | 197 |
It is interesting to note that while modernBERT reserves tokens for longer number sequences, and a lot more tokens for 3-digit numbers, it has clearly less of them for 4-digit numbers. Again, most of the 4-digit numbers in the ModernBERT vocabulary are year numbers from the recent centuries, especially 1930-2030.
-
It did require a bit of troubleshooting and rewriting though. Since interestingly enough, ModernBERT has 50368 input embedding vectors, but only 50280 tokens. One wonders what the 88 other ones are for? ↩