In my previous post I wrote about the context-free embeddings of the ModernBERT model, especially in comparison with the vanilla BERT. While we looked at the embedding vectors themselves, I also ended up plotting the distribution of lengths of the tokens¹ in each model:

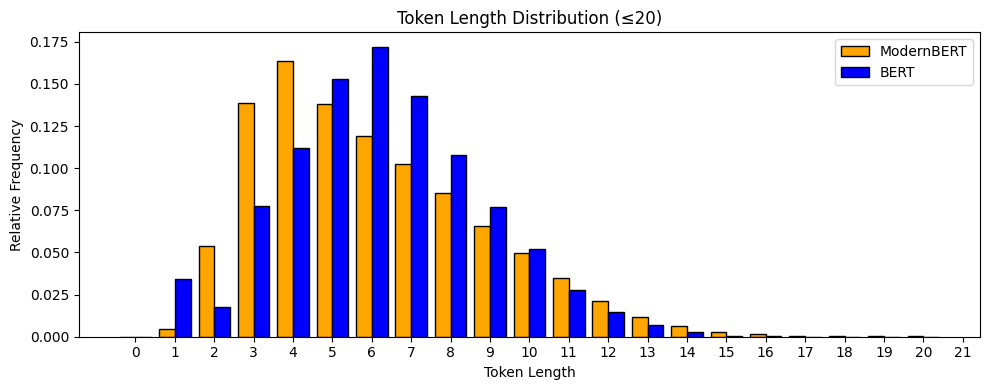
The ModernBERT model has almost double the amount of vocabulary (50k vs 30k) compared to the vanilla BERT model, and I wondered if the mass shifting right in the distribution is something to be expected. I decided to try this out, and used a combination of subsets of the Gutenberg corpus and Wikipedia data, totaling about 30Mb, to train tokenizers of various vocabulary sizes.

In this first image we see the distribution of tokens of tokenizers trained with a vocabulary size/budget of 1k to 9k. We can see a similar shift of distribution as observed in the 30k to 50k case of BERT vs ModernBERT.

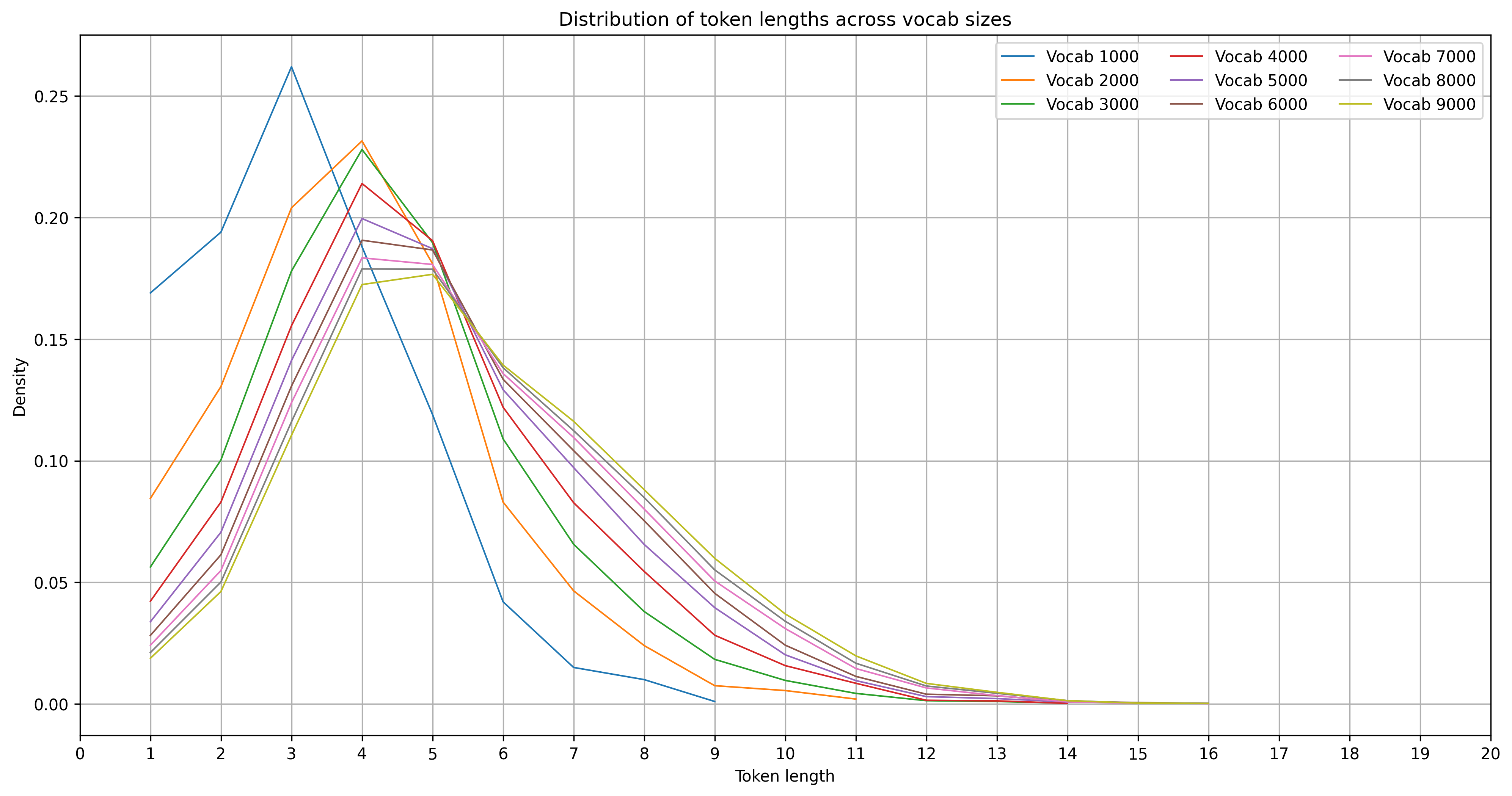
The default max vocabulary size for the transformer library's tokenizer system² seemed to be 82252, and the following image shows the distributions token lengths of 83 different tokenizers with vocabulary size in range(1000, 83000, 1000).

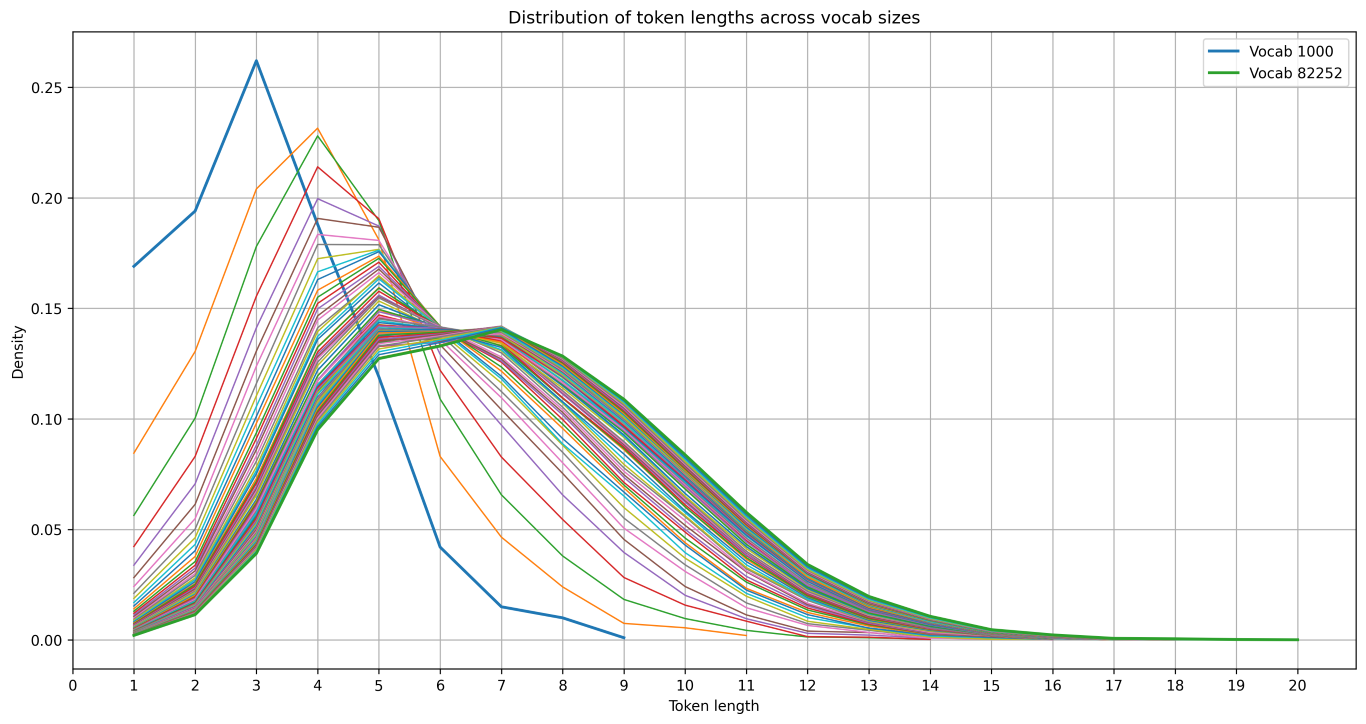
So indeed we see an almost continuous shift, and either convergence to a distribution or some more exponential/logarithmic effect that is not visible on our linear scale of experiments. To see the shift in more statistical terms, here are the evolutions of the max, mean, median and 90:th percentile token lengths, with the max evolution removed from the plot on the right.

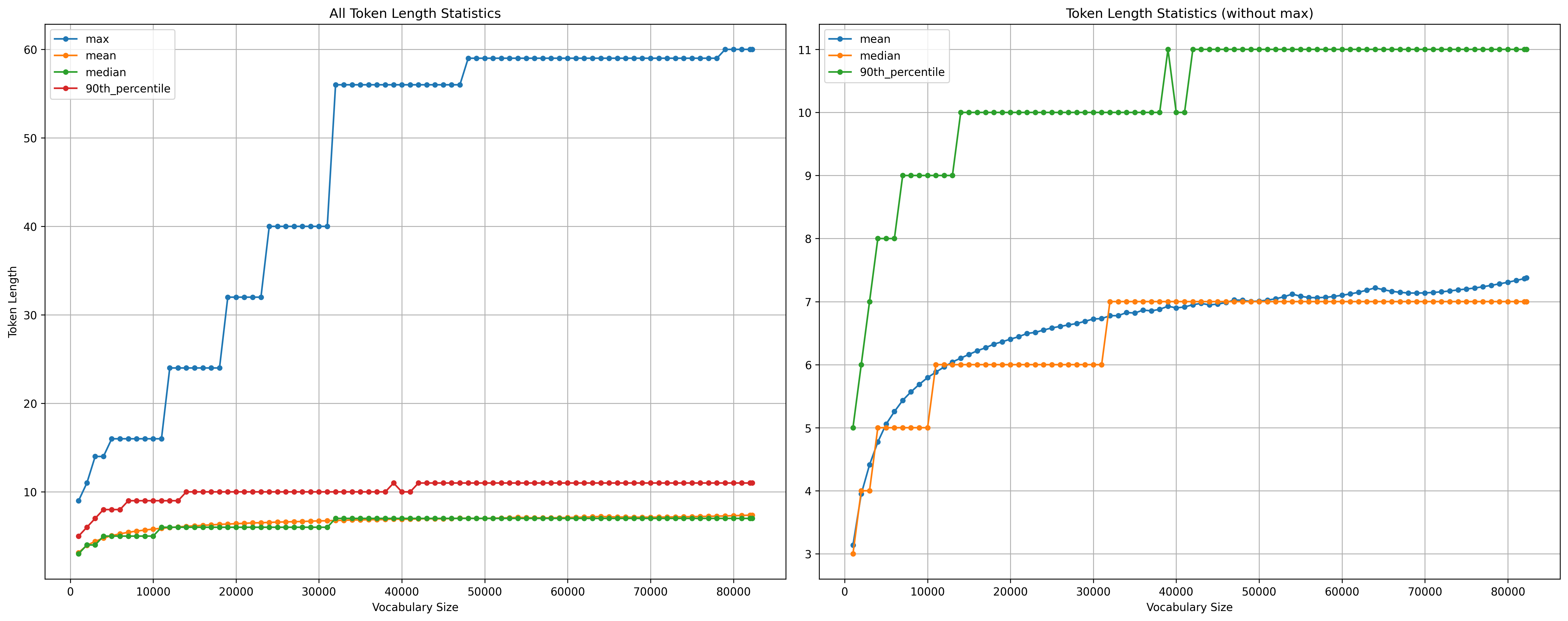
There is an interesting discontinuity on the behaviour of the median (and 90:th percentile) length which, I'm sure, would be obvious to me if I had studied BPE in more detail. The mean length looks most well-behaved, and thus I feel it reasonable to plot that in log scale:

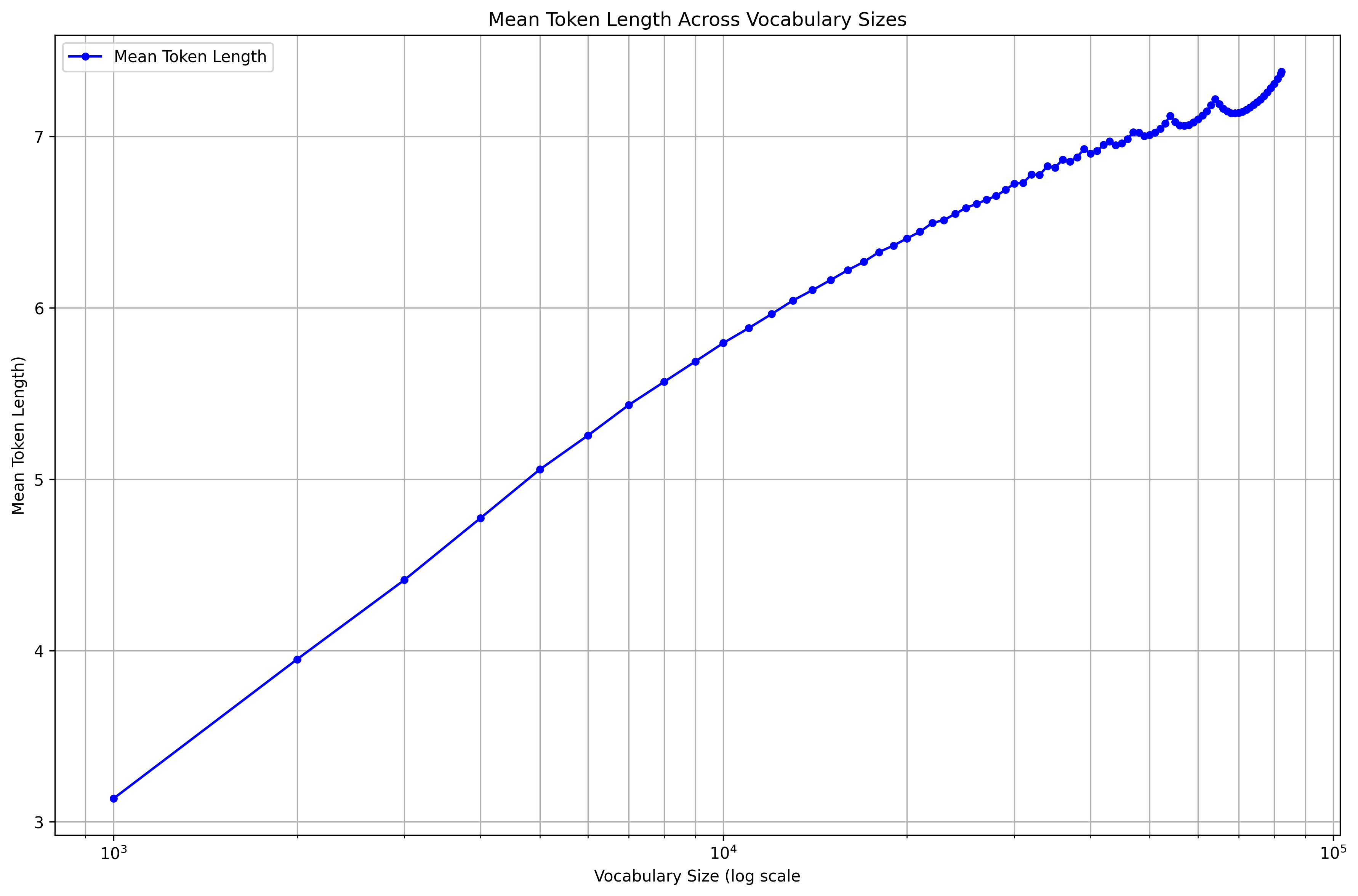
Again I am uncertain if this linearity is excpected or not.

We also note that the fact that we have been plotting the token length distributions on a relative scale does play a difference. Here we have the plots from before unrelativized:

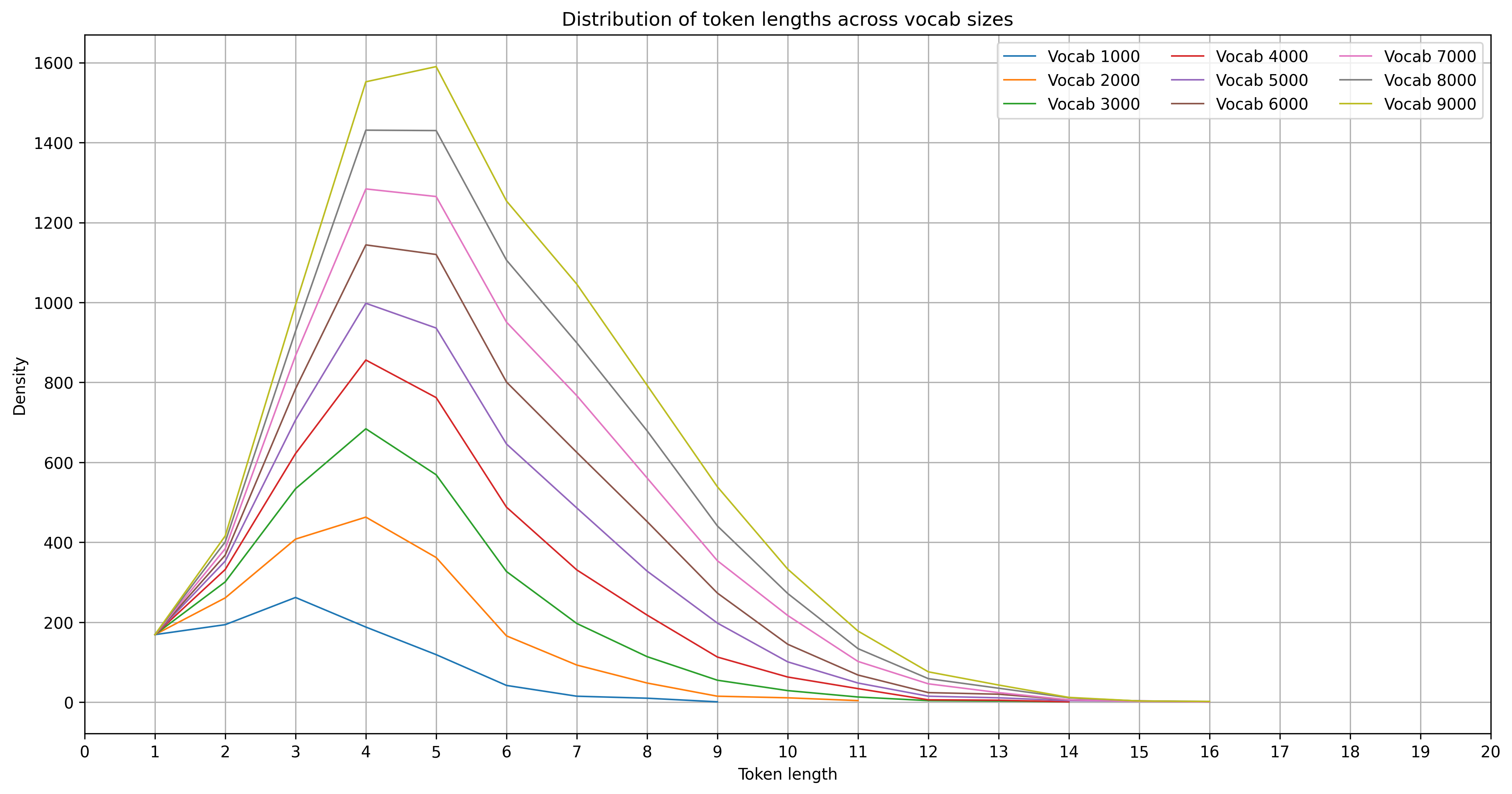
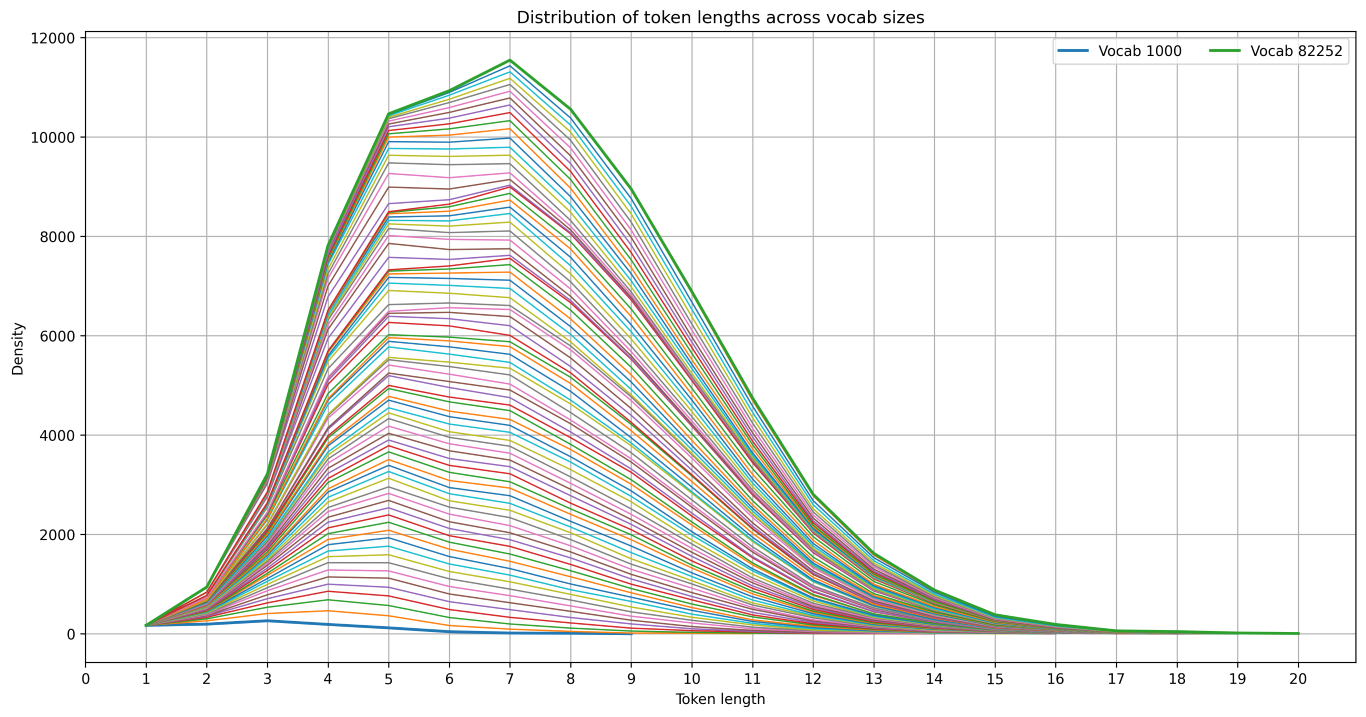
So in particular, more vocabulary tends to increase the amount of all lengths of tokens, but the increase is focused more on longer tokens when we have a larger vocabulary. This makes sense to me as there are more meaningful tokens with longer length. Also the idea of a tokenization is to build words out of components, and with more room for components the natural thing is to have more larger components. There must be a theorem hiding in here somewhere.

Again, but with more data?

After these observations, it's natural to get suspicious on what all of this is simply the result of me fitting a tokenizer to a dataset of about 23Mb. So I upped my dataset to 20Gb and set the tokenizer trainer script running. It seems to be melting my CPU but I'll write some sort of update once I get results.